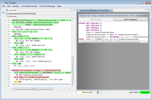
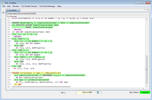
Hierarchical proofs

Our proof requires the following properties of GCDs, which for simplicity we just assume:

Known and usable facts

At any point in a TLA+ proof, there is a current obligation that is to be proved. The obligation contains a context of known facts, definitions, and declarations, and a goal. The obligation claims that the goal is logically entailed by the context. Some of the facts and definitions in the context are marked as usable for reasoning, while the remaining facts and definitions are hidden. That obligation is then sent to a backend (Zenon, Isabelle, SMT solvers – see the tactics section) that tries to prove it. The smaller the context is, the faster those backends are. Hence TLAPS tries to keep that context as small as possible. For example, the axioms about GCD stated above are not directly usable by the backends: they are known but not usable. As we have seen in the simple proof section, you have to explicitly USE or cite a fact in order for it to be included in the context of the obligation sent to backends. As an exception to this rule, domain facts of the form x \in S are always usable in a proof. (Such assumptions are typically introduced in an ASSUME … PROVE construct, most frequently in the form of an assumption NEW x \in X.) Moreover, unnamed proof steps (see below) are aways usable. The other known facts are hidden by default.

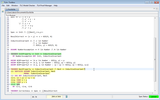
Let us get back to our example. Now that we have proved that the initial state satisfies the invariant, let us prove that this invariant is preserved by the next-state relation Next

SUFFICES

Let us first simplify the goal to be proved by using a SUFFICES construct:

This step asserts that it is sufficient to prove InductiveInvariant' while assuming InductiveInvariant and Next. Because the step is unnamed, both facts InductiveInvariant and Next are also made usable for the remainder of the proof. For more information about SUFFICES, see the section about other proof constructs.

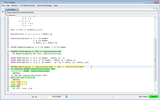
USE

We'll need the definitions of InductiveInvariant and Next to be usable in the entire body of the proof. Hence, rather than making them usable with a BY DEF construct in each step, we can make them usable for all proof steps by using the USE DEF construct once, at the beginning of the proof:

The general form of a USE step is:

USE e₁, …, e_m DEF d₁, …, d_n

which asserts that the definitions d₁, … d_n are to be made usable, and the facts e₁, …, e_m are to be checked and then added to the context as usable. When checking these facts, all other known facts are temporarily considered to be usable, so it is possible to say USE e /\ f when e and f are in the context but hidden. Observe that the USE directive is syntactically similar to BY, but it obviously does not check if the current assertion follows from the cited facts.

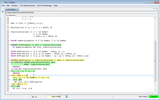
The QED step

To prove the theorem NextProperty, we have to reason by cases, and prove that InductiveInvariant' is true when one of the actions of Next is performed (i.e. when x < y and also when x > y). Let us write this outer level of the hierarchical proof:

<1>1, <1>a, <1>b and <1>2 are step names (the <1> part of the step name indicates the step's level, which is 1. The proof itself consists of four claims named by these step names (plus the two first unnamed steps); the first three are unjustified, while the last is justified by the cited facts <1>1, <1>a and <1>b. The QED step asserts the main goal of the theorem. Let us verify that it can be proved from steps <1>1, <1>a and <1>b:

After having asked TLAPS to prove the theorem, the QED step gets colored green. This means that facts mentioned by steps <1>1, <1>a and <1>b are sufficient to prove the theorem. But as you can see, those proof steps are colored yellow, which means that their proofs are omitted. (The Toolbox allows you to change what colors are used to indicate the proof status of a step, and also what proof statuses are displayed.) Let us now prove these proof steps.

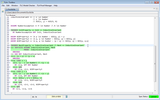
Non-QED steps

First, the proofs of the SUFFICES step and step <1>1 are obvious as you can see in the following screenshot. In particular, step <1>1 follows from the usable fact Next introduced in the unnamed SUFFICES step and the definition of Next, which is also usable.

Let us now prove step <1>a. We subdivide this proof into two steps of level 2. The first step asserts that y - x \in Number and that y is not less than x. The second, QED step proves the main goal from the case assumption of step <1>a, the just established step <2>1, and axiom GCDProperty3.

Let us now prove step <2>1. We have to use the case assumption <1>a and make the definition of Number usable:

The proof of the y < x case is quite similar:

Then theorem NextProperty is proved by TLAPS:

Wrapping up the proof

Now we have InitProperty and NextProperty, we can prove the main theorem.

First we prove that a stuttering step (i.e. a step that leaves all variables unchanged) keeps the invariant unchanged. This is proved simply by checking that the definition of InductiveInvariant involves no variables other than x and y:

Then we can prove that any process that follows the specification must keep InductiveInvariant true at all times, by using the previous step and the InitProperty and NextProperty theorems:

Unfortunately, that doesn't work:

Indeed, none of the default back-end provers (SMT, Zenon, and Isabelle) can deal with temporal logic. But TLAPS includes an interface to a propositional temporal logic prover (LS4), which can be invoked by adding PTL to the set of usable facts. Since PTL is defined in the TLAPS.tla standard module, we have to explicitly extend the TLAPS module:

Then we can use the PTL backend to prove step <1>2:

Finally we prove that, at any point in time, our invariant entails the correctness of the result, then use that to prove the main theorem:

And this concludes the proof of correctness of Euclid's algorithm.

Summary

This is the whole file, with the specification and proofs: