Advanced options

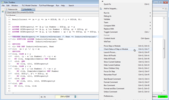
Status checking

The Toolbox remembers the coloring of proof steps. It can be very useful when re-opening a module to know quicky what has been already proved and what has not. However, the color used by the Toolbox to highlight a proof step reflects the step's proof status the last time TLAPS checked the proof. This status may be obsolete if you have edited the proof since then. You can check the current status of a proof step (and of all its substeps) by clicking and then right-clicking on the step (or use the ctrl+G,ctrl+T / cmd-G,cmd-T shortcut), as shown in the following screenshot:

Proving an obligation can take time, but checking its status is pretty fast. (It is not instantaneous because the obligations still have to be computed.) It's a good idea to check the proof status of the complete theorem from time to time, since changing some step could change a later proof obligation, making its previous status no longer meaningful. You can edit your file while the Toolbox is checking proof statuses. (The file is read-only while a proof is in progress.) You can instruct TLAPS to check the status of (or to prove) all theorems in the file by giving the usual command when the cursor is outside any theorem or its proof.

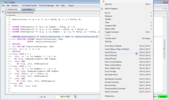
Prover options

If you don't use tactics, the default behaviour of TLAPS is to send obligations to Z3, then to Zenon, then to Isabelle, stopping when one of them succeeds. You can change this behavior, by clicking on "Launch Prover" when right-clicking on a proof-step:

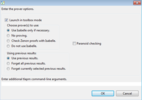
As you can see, you can either ask TLAPS not to prove obligations (that's similar to status checking), or ask TLAPS to make Isabelle check proofs provided by Zenon.

You can also ask TLAPS to forget previous results about obligations of a particular proof-step or the entire module.

Finally, you can specify command-line options that will be added to the ones normally used by the Toolbox when it launches tlapm. The most useful options are the following:

• --threads n : change the maximum number of back-end provers that are launched in parallel. The default is the number of CPU cores on your machine.
• --method list : change the default list of back-end provers for BY and OBVIOUS steps. The argument is a comma-separated list of methods. The following methods are available:

  name	method
  zenon	Zenon
  auto	Isabelle with tactic auto
  blast	Isabelle with tactic blast
  force	Isabelle with tactic force
  smt	baseline SMT solver (by default Z3)
  z3	Z3
  cvc4	CVC4

• --solver line : change the baseline SMT solver. See Tactics for instructions on using this option.
• --fast-isabelle : on Windows, invoke Isabelle via a short-cut that saves a few seconds from Isabelle's start-up time. On other architectures, this option does nothing.
• --stretch f : multiply all timeouts by a factor of f. This is particularly useful when using a slower machine to re-check proofs made on a faster machine.

The internal processing that the program tlapm performs is shown in the following diagram. tlapm reads a TLA+ file (or TLA+ files), parses it, applies a number of transformations, and at some point converts to formats that can be used to communicate with external solvers (these are other programs). These solvers include:

• an SMT solver ( z3, cvc4, veriT, or other),
• the automated theorem prover zenon,
• the proof assistant Isabelle with the formalization of TLA+ (Isabelle files),
• and the propositional temporal logic prover ls4 via the interface program ptl_to_trp.

Depending on what these external solvers return to tlapm, tlapm outputs to the TLA+ Toolbox , and to stdout and stderr, which parts of the proof tlapm could successfully prove, and which parts not. This output indicates which parts of the proof need further changes, e.g., by adding more details to the proof, or by changing what we are attempting to prove.

The internal transformations within tlapm include:

• the generation of proof obligations, which can be thought of as individual "theorems" that tlapm needs to prove in order to prove the entire module (not to be confused with THEOREM statements in the TLA+ source file),
• the normalization of expressions and expansion of defined operators by their definiens,
• the interpretation of the operators ENABLED and \cdot,
• the computation (and later saving) of fingerprints of proof obligations (to remember proof results and skip reproving them in later invocations of tlapm), and
• coalescing.

For each proof step, more than one proof obligation may be generated. Among the proof obligations that are generated from a proof step, there is one proof obligation that has as consequent the same consequent as that proof step in the TLA+ source. The other proof obligations that are generated from that same proof step have as consequents the facts that are listed in the BY statement of that proof step (i.e., the identifiers and expressions listed within the BY statement before the keyword DEF).