Preamble

TLAPS is a proof system for checking TLA+ proofs. See the TLA Home page to learn about the TLA+ specification language. The proof language is a new addition to TLA+; it is described here. However, this is a reference manual; you should try some examples before reading it.

This tutorial consists of a simple example. If you have no experience with TLA+ or using theorem provers, you might start instead with the TLA+ Hyperbook or the TLA+ Video Course. This tutorial will introduce concepts of the TLA+ proof language as needed.

The proof system is designed to be used with the ToolBox IDE. In this tutorial, we assume that you are using that IDE (even if we sometimes indicate how proofs can be run from the command line).

The example

Broadly speaking, a TLA+ proof is a collection of claims, arranged in a hierarchical structure which we describe below, where each claim has an assertion that is either unjustified or justified by a collection of cited facts. The purpose of TLAPS is to check the user-provided proofs of theorems, that is, to check that the hierarchy of claims indeed establishes the truth of the theorem if the claims were true, and then to check that the assertion of every justified claim indeed is implied by its cited facts. If a TLA+ theorem has a proof with no unjustified claims, then, as a result of checking the proof, TLAPS verifies the truth of the theorem.

We shall illustrate the TLAPS by proving the correctness of the Euclidean algorithm.

The algorithm

The well-known Euclidean algorithm can be written in the PlusCal language as follows:

The PlusCal translator translates this algorithm into a TLA+ specification that we could prove correct. However, in this tutorial, we shall write a somewhat simpler specification of Euclid's algorithm directly in TLA+.

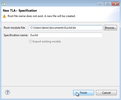
Creating a new TLA+ module

First of all, let us create a new specification within the ToolBox (click on the thumbnails to expand the screenshots).

Importing modules

In order to get the definitions of arithmetic operators (+, -, etc.), we shall make this specification extend the Integers standard module.

Definitions

We shall then define the GCD of two integers. For that purpose, let us define the predicate "p divides q" as follows:
p divides q iff there exists some integer d in the interval 1..q such that q is equal to p times d.

We then define the set of divisors of an integer q as the sets of integers which both belong to the interval 1..q and divide q:

We define the maximum of a set S as one of the elements of this set which is greater than or equal to all the other elements:

And finally, we define the GCD of two integers p and q to be the maximum of the intersection of Divisors(p) and Divisors(q):

For convenience, we shall also define the set of all positive integers as:

When we save the specification (with the menu File > Save), the toolbox launches the SANY syntactic analyzer and reports any errors that might appear.

Constants and variables

We then define the two constants and two variables needed to describe the Euclidean algorithm, where M and N are the values whose GCD is to be computed:

The specification

We define the initial state of the Euclidean algorithm as follows:

In the Euclidean algorithm, two actions can be performed:

• set the value of y to y - x if x < y
• set the value of x to x - y if x > y.

These actions are again written as a definition called Next, which specifies the next-state relation. In TLA+, a primed variable refers to its value at the next state of the algorithm.

The specification of the algorithm asserts that the variables have the correct initial values and, in each execution step, either a Next action is performed or x and y keep the same values:

(For reasons that are irrelevant to this algorithm, TLA specifications always allow stuttering steps that leave all the variables unchanged.)

We want to prove that the algorithm always satisfies the following property:

Hence we want to prove the following theorem named Correctness:

Summary